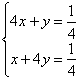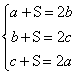Autor: BOŻENA CHRAMĘGA
nauczyciel matematyki
w Gimnazjum nr 24 w Krakowie
ZBIÓR ZADAŃ
DLA UCZNIÓW UZDOLNIONYCH
MATEMATYCZNIE
/z rozwiązaniami/
ZAD. 1.
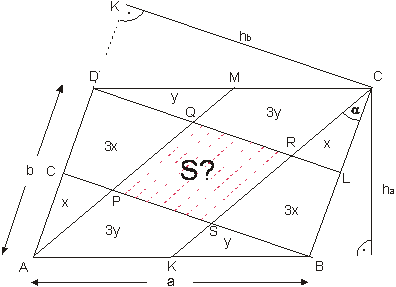
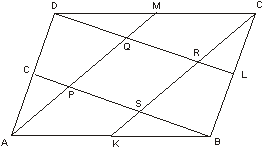
Dany jest równoległobok ABCD o polu 1. Środki boków /p-kty K,L,M,N/ połączono z wierzchołkami równoległoboku jak na rysunku. Wewnątrz równoległoboku powstał czworokąt PQRS. Oblicz pole tego czworokąta.
![]()
|
|
P |
|
|
i
∆CRL ~ ∆CSB /∢α wspólny/
k=2
P∆CSB = 4 P∆CRL = 4x ß P = - P∆CRL P Analogiczne zależności występują dla par trójkątów podobnych: ∆ANP ~ ∆ADQ ∆DQM ~ ∆DRC ∆KSB ~ ∆APB |
P S + 8x +8y = 1 S +8(x+y) = 1 S=1-8(x+y) P∆KBC = = P∆KBC = 4x + y P∆ANB = = P∆ANB = x + 4y |
|
|
S = 1 – 8
(x +y) S = 1 – 8
× S = 1 –
Odp. Szukane pole czworokąta PQRS wynosi |
|
|
|
|
|
|
ZAD. 2.
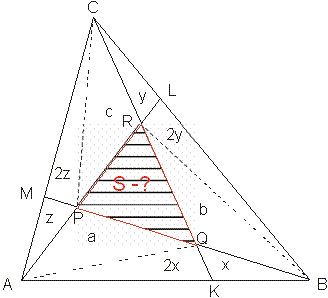
Dany jest trójkąt ABC o polu 1. Każdy bok trójkąta dzielimy na 3 równe części. Otrzymujemy p-kty K, L, M takie, że:
![]()
![]()
![]() Rysujemy odcinki
Rysujemy odcinki ![]() ,
, ![]() ,
, ![]() . Powstał trójkąt PQR.
. Powstał trójkąt PQR.
Oblicz jego pole.
![]()
|
|
P |
|
P /Trójkąty mają tą samą wysokość; podstawa Analogicznie: P i P P P P P 3x + 3y + 3z + a + b + c + S = 1 I. 3 (x +
y + z) + a + b + c + S = 1 Rozpatruję DAKR i DKBR: P /Trójkąty mają tą samą wysokość; podstawa 2x + a + S = 2(x + b) (1) a + S = 2b Analogicznie: rozpatruję DBLP i DCLP: P 2y + b + S = 2(y + c) |
(2) b + S = 2c rozpatruję DCMQ
i DAMQ: 2z + c + S = 2(z + a) (3) c + S = 2a Dodaję stronami równania (1), (2), (3): 3S + a + b + c = 2a
+ 2b + 2c 3S = a + b +
c
Rozpatruję DAKC i DKBC: P 3z + 2x + a + c + S = 2(3y + b + x) (4) 3z + a + c + S = 2b + 6y Rozpatruję DBLA i DLCA: P 3x + 2y + a + b + S = 2(3z + y + c) (5) 3x + a + b + S = 6z + 2c Rozpatruję DCMB i DAMB: 3y +2z + c + b + S = 2(3x + a + z) |
(6) 3y + c + b + S = 6x
+ 2a
Dodaję stronami 4), 5), 6):
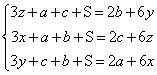
![]()
3(x + y
+ z) + 2a + 2b + 2c + 3S = 2a
+ 2b + 2c + 6(x + y + z)
3S = 6(x + y + z) – 3(x + y + z)
3S = 3(x + y + z) / :3
S = x +
y + z
I. 3(x + y + z) + a + b + c + S = 1
3 S + 3S + S = 1
7S = 1 / :7
S
= ![]()
Odp. Szukane pole trójkąta PQR wynosi ![]() .
.
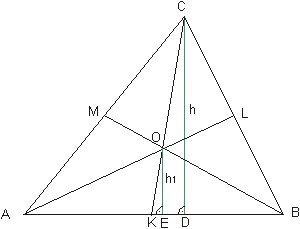
ZAD. 3.
W trójkącie ABC poprowadzono środkowe przecinające środkowe przecinające się
w punkcie O. Wykaż, że każdy z 6 powstałych trójkątów ma takie samo pole.
![]()
|
|
K, L, M – środki boków DABC
P /Trójkąty mają tą samą podstawę równą Analogicznie: P P |
Rozpatruję DABO:
Na podstawie tw. Talesa i własności środkowych trójkąta:
![]()
![]()
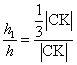 Þ
Þ ![]()
P![]() ABO=
ABO=
![]() = P
= P![]() ABC
ABC
Ponieważ P![]() AKO
= P
AKO
= P![]() KBO i P
KBO i P![]() ABO
= P
ABO
= P![]() AKO
+ P
AKO
+ P![]() KBO
KBO
![]() P
P![]() ABC
= 2P
ABC
= 2P![]() AKO
/ ·
AKO
/ ·![]()
P![]() AKO
=
AKO
= ![]() P
P![]() ABC
ABC
P![]() KBO =
KBO = ![]() P
P![]() ABC
ABC
Analogicznie wykazuję, że
W DCBO: P![]() BLO
= P
BLO
= P![]() LCO
=
LCO
= ![]() P
P![]() ABC.
ABC.
W DACO: P![]() CMO
= P
CMO
= P![]() AMO =
AMO = ![]() P
P![]() ABC.
ABC.
Z tego wynika, że P![]() AKO
= P
AKO
= P![]() KBO
= P
KBO
= P![]() BLO
= P
BLO
= P![]() CLO
= P
CLO
= P![]() MOC = P
MOC = P![]() AMO =
AMO = ![]() P
P![]() ABC,
więc każdy z sześciu trójkątów ma takie samo pole.
ABC,
więc każdy z sześciu trójkątów ma takie samo pole.
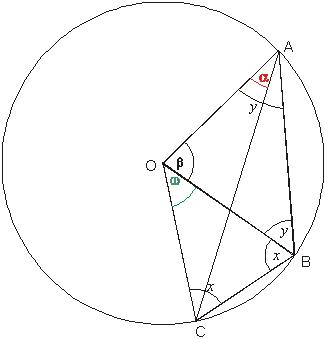
ZAD. 4.
Dane są punkty A,B,C leżące na okręgu o środku O. Rysujemy czworokąt ABCO. Rysujemy przekątne czworokąta znając |∢BOC| = ω i |∢OAC| = α wyznacz miary katów czworokąta ABCO.
![]()
|
|
|
||
|
DCBO jest równoramienny |∢OCB|
= |∢COB| = x 2x + ω = 180o
DACO jest równoramienny |∢ACO| = |∢OAC| = α |∢AOB|
= β 2α + ω + β = 180o
DABO jest równoramienny |∢OAB| = |∢ABO| = y 2y + β = 180o 2y = 180o – β 2y = 180o – (180o – 2α –
ω) |
2y = 2α + ω /:2 W czworokącie ABCO: |∢OAB|
= y
|∢ABC|
= x + y = 90o – |∢ABC| = 90o
+ α |∢BCO|
= x
|∢ACO| = ω + β = ω + 180o – 2α – ω |∢AOC| = 180o
+ 2α |
Spr.
|∢OAB|
+ |∢ABC| + |∢BCO| + |∢AOC| = 360o
![]() + α + 90o
+ α + 90o –
+ α + 90o
+ α + 90o – ![]() ω + 180o – 2α = 360o
ω + 180o – 2α = 360o
360o = 360o
L = P
Odp. Kąty wewnętrzne czworokąta ABCO mają miary: α + ![]() ω; 90o + α; 90o –
ω; 90o + α; 90o – ![]() ω
ω
i 180o – 2α
ZAD. 5.
Niech a + b = 1 i a2 + b2 = 2.
![]() Oblicz a4 + b4
.
Oblicz a4 + b4
.
a + b = 1 |2
(a + b)2 = 1
![]() a2 + b2 + 2ab= 1
a2 + b2 + 2ab= 1
2 + 2ab = 1
2ab = –
1 /:2
ab = ![]() |2
|2
a2b2 = ![]()
(a2 + b2)2 = 22 =
4
a4 + 2a2b2 + b4
= 4
a4 + b4 = 4 – 2a2b2
a4 + b4 = 4 – 2 · ![]()
a4 + b4 = 4 – ![]()
![]()
Odp. Wartość wyrażenia a4 + b4
wynosi 3![]()